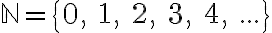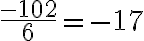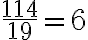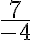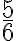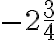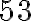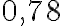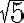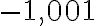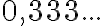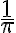Lukujoukot

LUONNOLLISTEN LUKUJEN JOUKKO 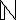$\mathbb {N}$

muodostuu luvuista 0, 1, 2, 3, 4, . . ., mikä merkitään hakasuluilla

$\mathbb{N}=\left\{0{,}\ 1{,}\ 2{,}\ 3{,}\ 4{,}\ ...\right\}$.

Tämä tarkoittaa, että joukkoon kuuluvat 0 ja sitä suuremmat kokonaisluvut. Luonnollisia lukuja on äärettömän paljon (loputtomasti), koska kun arvelet löytäneesi suurimman mahdollisen kokonaisluvun, voit aina kuitenkin lisätä siihen luvun 1 ja saada seuraavan luonnollisen luvun. Luonnollisten lukujen joukkoa voidaan havainnollistaa lukusuoralla:

Kun kaksi luonnollista lukua lasketaan yhteen tai kerrotaan keskenään, summa ja tulo ovat edelleen luonnollisia lukuja.

$72+1008=1080$                                                            $35 \cdot 20=700$

$0+31=31$                                                                        $0 \cdot 16=0$

Vähennyslasku saattaa sen sijaan aiheuttaa ongelmia: $72 - 18 =54$, mutta entä  $18-54$?

Tämä vähennyslasku on mahdollinen, kun käytetään Kokonaislukujen joukkoa $\mathbb {Z}$

KOKONAISLUKUJEN JOUKKO $\mathbb {Z}$

muodostuu kaikista kokonaisluvuista  

$\mathbb{Z}=\left\{... , -5, -4, -3, -2, -1 , 0, 1, 2, 3, 4, 5, ...\right\}$

Kokonaislukujen joukko voidaan myös esittää lukusuoralla

Kokonaislukujen joukkoon kuuluvat siis kaikki luonnolliset luvut ja niiden vastaluvut

VASTALUKU

Luvun ja sen vastaluvun summa on 0.

Yleisesti: luvun a vastaluku on - a, koska 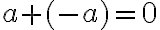$a+(-a)=0$

Vastaluvun löydät merkitsemällä luvun eteen - merkin. Esimerkiksi luvun 7 vastaluku on -7 ja luvun -10 vastaluku -(-10) = 10.

Luvun -c vastaluku on -(-c) = c ja luvun 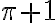$\pi+1$ vastaluku  $-( \pi+1)=- \pi-1$.

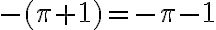Kokonaislukujen summa, erotus ja tulo ovat aina myös kokonaislukuja. Sen sijaan osamäärän suhteen saattaa tulla ongelmia:

Esimerkiksi $\frac{-102}{6}=-17$  ja  $\frac{114}{19}=6$ , mutta entä  $\frac{7}{-4}$ ?

RATIONAALILUVUT 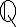$\mathbb{Q}$

Jokaisen rationaalilukujen joukkoon 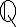$\mathbb{Q}$ kuuluvan luvun voi ilmaista murtolukuna 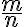$\frac{m}{n}$,  missä osoittaja m ja nimittäjä n ovat kokonaislukuja ja $n \neq 0$.

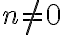Mieti, mitkä seuraavista luvuista voit ilmaista murtolukumuodossa eli mitkä niistä siis ovat rationaalilukuja. Ratkaisun löydät alla olevasta ratkaisutiedostosta.

a)  $\frac{5}{6}$

b)  $-2 \frac{3}{4}$

c)  $53$

d)  $0,78$

e)  $\sqrt{5}$

f)  $-1,001$

g)   $0,333 . . .$

h)  $\frac{1}{ \pi }$

i)  $-4$

Alla on linkki Ville Sahimaan YouTube-videoon, jossa selviää, miten päättymättömän desimaaliluvun saa muutettua murtolukumuotoon, jos se on jaksollinen. Päättymättömät jaksolliset desimaaliluvut ovat siis rationaalilukuja. Sen sijaan päättymättömiä jaksottomia desimaalilukuja ei voi kirjoittaa murtolukumuotoon, ja ne ovatkin irrationaalilukuja.

REAALILUVUT 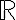$\mathbb {R}$

Rationaaliluvut ja irrationaaliluvut yhdessä muodostavat reaalilukujen joukon 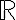$\mathbb {R}$ . Reaaliluvut täyttävät koko lukusuoran. Se tarkoittaa, että jokaista lukusuoran pistettä vastaa reaaliluku ja jokaista reaalilukua piste lukusuoralla.

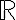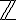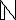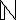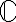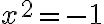Lukiossa matematiikan tehtävissä käytetään perusjoukkona reaalilukujen joukkoa $\mathbb {R}$ , jos ei muuta ole mainittu. Poikkeuksena ovat mm. Lukuteoria $\mathbb{Z}$ tai $\mathbb {N}$ ja lukujonojen indeksit $\mathbb {N}$. Syventävillä kursseilla voidaan myös tarvita kompleksilukujen joukkoa $\mathbb {C}$, josta voidaan mm. löytää ratkaisu yhtälölle  $x^2 = -1$.