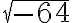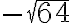Neliö- ja kuutiojuuri
Neliö- ja kuutiojuuri
NELIÖJUURI
Määritelmä
(MAOL-taulukosta)
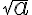 on sellainen ei-negatiivinen luku, jonka neliö (toinen potenssi) on a.
on sellainen ei-negatiivinen luku, jonka neliö (toinen potenssi) on a.
Tässä neliöjuurimerkin alla olevaa lukua a sanotaan juurrettavaksi.
Määritelmässä on siis kaksi ehtoa:
Tämä tarkoittaa, että esimerkiksi
Koska juurrettava on neliöjuuren toinen potenssi, neliöjuurella on määrittelyehto: minkään reaaliluvun toinen potenssi ei ole negatiivinen, joten negatiivisille luvuille ei löydy neliöjuurta. Määrittelyehto on siis: juurrettava 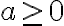 .
.
Neliöjuurilla laskemista helpottaa potenssien laskusääntöjä muistuttavien neliöjuuren laskukaavojen tunteminen. Tutustutaan tässä kolmeen tärkeimpään
Neliöjuurten laskukaavat
Kaavat toimivat molempiin suuntiin, vasemmalta oikealle ja oikealta vasemmalle.
Kaavan 1 mukaan voidaan laskea esimerkiksi: 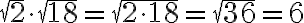
Kaavaa 2 sovelletaan mm. murtolukujen neliöjuurissa:
Kaavan 3 oikean puolen itseisarvomerkit voivat ensinäkemältä näyttää turhilta, mutta kun ajattelemme reaalilukua a, sillä on yhtä suuret mahdollisuudet oilla positiivinen tai negatiivinen. Olipa se kumpi vain, sen toinen potenssi 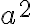 on nolla tai positiivinen luku ja täyttää neliöjuuren määrittelyehdon. Kun tästä otetaan neliöjuuri, sen on oltava
on nolla tai positiivinen luku ja täyttää neliöjuuren määrittelyehdon. Kun tästä otetaan neliöjuuri, sen on oltava 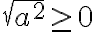 , ja varmasti tämän ehdon täyttää
, ja varmasti tämän ehdon täyttää 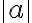 . Esimerkiksi luku
. Esimerkiksi luku 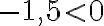 , mutta
, mutta 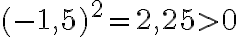 . Voimme ottaa neliöjuuren
. Voimme ottaa neliöjuuren 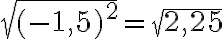 , josta ei tässä tapauksessa tule alkuperäistä lukua -1,5 vaan sen itseisarvo
, josta ei tässä tapauksessa tule alkuperäistä lukua -1,5 vaan sen itseisarvo 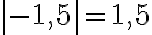
KUUTIOJUURI (kolmas juuri)
Määritelmä:
![\sqrt[3]{a} \sqrt[3]{a}](https://edugo.fi/filter/tex/pix.php/27af11e322a7d86181aa6abae738ed04.gif) tarkoittaa lukua, jonka kolmas potenssi on a.
tarkoittaa lukua, jonka kolmas potenssi on a.
Koska negatiivisten lukujen kolmannet potenssit ovat negatiivisia, myös negatiivisilla luvuilla on kolmas juuri. Ylläolevista neliöjuuren laskukaavoista 1. ja 2. ovat myös kuutiojuuren laskukaavoja.
Vain harvojen reaalilukujen neliö- tai kuutiojuuret ovat kokonaislukuja tai edes murtolukuja. Silloin tarkka arvo on juurilauseke, esim, 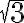 tai
tai ![\sqrt[3]{12} \sqrt[3]{12}](https://edugo.fi/filter/tex/pix.php/c016c61a8932001476d304b30c6588f4.gif) . Likiarvon saat laskimesta. Potenssiyhtälöiden yhteydessä tässä osiossa on video, jossa näytetään, miten geogebran CAS-laskimella saa otettua juuren likiarvon.
. Likiarvon saat laskimesta. Potenssiyhtälöiden yhteydessä tässä osiossa on video, jossa näytetään, miten geogebran CAS-laskimella saa otettua juuren likiarvon.
Pohdi seuraavia esimerkkejä. Ratkaisut löytyvät tarvittaessa allaolevasta ratkaisutiedostosta.
Esimerkki 1. Sievennä
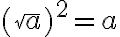
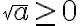
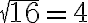
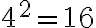
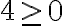
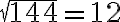
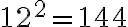
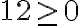
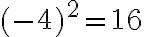
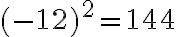
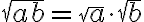
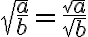
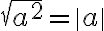
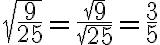
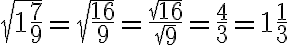
![\sqrt[3]{27} = 3 \sqrt[3]{27} = 3](https://edugo.fi/filter/tex/pix.php/0f08a4a97b3ed0bd8803a416ede2f3a8.gif)
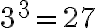
![\sqrt[3]{-8} = -2 \sqrt[3]{-8} = -2](https://edugo.fi/filter/tex/pix.php/13c04e9779e899472b6b30e86037b3d0.gif)
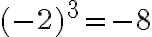
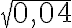
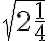
![\sqrt[3]{ \frac{2}{16} } \sqrt[3]{ \frac{2}{16} }](https://edugo.fi/filter/tex/pix.php/f8a407574133a95cd6cebea309338427.gif)
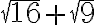
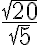
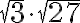
![\sqrt[3]{27000} \sqrt[3]{27000}](https://edugo.fi/filter/tex/pix.php/4372b1ad1fe30e493cc9c975f3f752f9.gif)
![\sqrt[3]{-64} \sqrt[3]{-64}](https://edugo.fi/filter/tex/pix.php/8a7af8a69db580ea120f87f32a2ca6d8.gif)