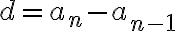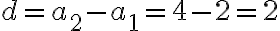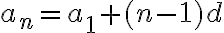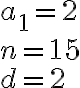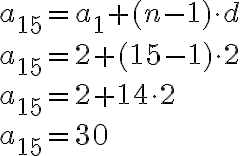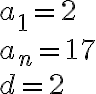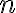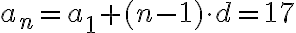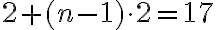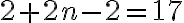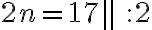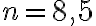Sivu
Aritmeettinen lukujono
Aritmeettinen lukujono
Suorituksen vaatimukset
Aritmeettisessa lukujonossa peräkkäisten jäsenten etäisyys toisistaan on aina yhtä suuri.
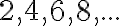
Lukujonon jäsenten etäisyyttä toisistaan kutsutaan erotusluvuksi eli differenssiksi.
Tässä esimerkkijonossa
Aritmeettisen lukujonon yleiselle jäsenelle
Tästä saadaan ratkaistua ensimmäisen jäsenen ja erotusluvun avulla mikä tahansa aritmeettisen lukujonon jäsen.
Tämän esimerkkijonon viidestoista jäsen saadaan seuraavasti
Toisaalta voidaan tutkia mikä on jonkun luvun järjestysnumero tässä lukujonossa tai onko luku ylipäätään tämän jonon jäsen. Mahtaako luvulle 17 löytyä paikka tässä esimerkkijonossa?
Koska saatu järjestysnumero ei ole kokonaisluku, ei tarkasteltu luku kuulu tähän lukujonoon.
Tässä linkissä on Matikkamatskut video aritmeettisestä lukujonosta
Viimeksi muutettu: torstai 26. maaliskuuta 2020, 11.59