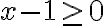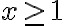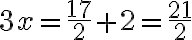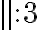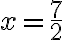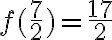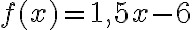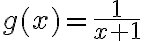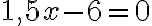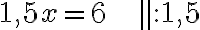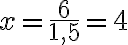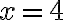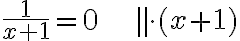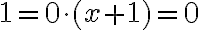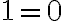Funktio
Funktio
Funktio liittää sovitun säännön mukaan jokaiseen määrittelyjoukon muuttujan arvoon tasan yhden luvun, funktion arvon.
Sääntö kuvaa muuttujan x ja funktion arvon y välistä riippuvuutta, se kertoo, miten x ja y liittyvät toisiinsa.
Esim. 1. Mitä alla olevien funktioiden muuttujan arvolle tapahtuu, että saadaan funktion arvo? Mikä on siis funktion sääntö?
a) funktio f
| muuttujan arvo | funktion arvo |
|---|---|
| 1 | 0 |
| 4 | 3 |
| 6 | 5 |
Funktion arvot näyttävät liittyvän muuttujan arvoihin säännön ¨vähennetään muuttujan arvosta 1¨ mukaan.
b)
| muuttujan arvo | funktion arvo |
|---|---|
| 0 | 0 |
| -2 | -1 |
| 1 | 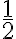 |
| 6 | 3 |
Luvuista päätellen funktion sääntö olisi ¨muuttujan arvo jaetaan luvulla 2¨.
FUNKTIOON LIITTYVIÄ MERKINTÖJÄ
Funktion nimi voi olla (ja usein onkin) muukin kirjain kuin f, samoin muuttujakirjaimen voit valita vapaasti. Esimerkiksi kartion tilavuuden riippuvuutta sen korkeudesta voisi kuvata funktio 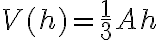 , jolloin funktion nimi on V ja muuttujakirjain on h.
, jolloin funktion nimi on V ja muuttujakirjain on h.
Funktion arvo halutulla muuttujan arvolla lasketaan sijoittamalla funktion lausekkeeseen muuttujan paikalle haluttu muuttujan arvo. Esimerkiksi alla kuvassa on laskettu funktion 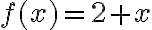 arvo muuttujan arvolla x = 7
arvo muuttujan arvolla x = 7
Esim. 2. Pohdi esimerkkiä. Ratkaisu tiedostona alla
a) Laske funktion 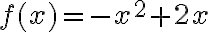 arvo, kun muuttuja x saa arvot
arvo, kun muuttuja x saa arvot 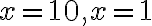 ja
ja 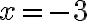
b) Laske funktion 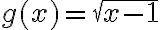 samoilla muuttujan x arvoilla.
samoilla muuttujan x arvoilla.
Funktion määritelmään liittyy se, että jokaista määrittelyjoukon lukua vastaa tasan yksi funktion arvo. Määrittelyjoukko tarkoittaa kaikkia niitä lukuja, joilla funktiolle voidaan laskea arvo, jos muuta ei ole mainittu. Voit myös määrittää määrittelyjoukon suppeammaksi, jos se sopii funktion käyttöön paremmin.
Esimerkin 2 funktiolle f on mahdollista määrittää arvo kaikilla reaaliluvuilla, kuten kaikille polynomifunktioille. Sen määrittelyjoukko on reaalilukujen joukko 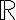 . Sen sijaan funktiolle g ei saada määritettyä arvoa, jos juurrettavan lausekkeen arvo on negatiivinen. Tästä seuraa määrittelyehto:
. Sen sijaan funktiolle g ei saada määritettyä arvoa, jos juurrettavan lausekkeen arvo on negatiivinen. Tästä seuraa määrittelyehto:
Lukion kursseilla perusoletus on, että funktioiden määrittelyjoukko olisi reaalilukujen joukko, ja poikkeustapaukset mainitaan erikseen.
Esim. 3. Millä muuttujan x arvolla funktio 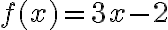 saa arvon
saa arvon 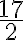 ?
?
Funktion arvo saadaan sijoittamalla muuttujan paikalle annettu arvo. Nyt tätä muuttujan arvoa ei tunneta, mutta funktion arvo, siis 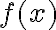 , on annettu. Saadaan yhtälö:
, on annettu. Saadaan yhtälö:
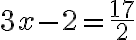 , josta muuttujan arvo x voidaan ratkaista:
, josta muuttujan arvo x voidaan ratkaista:
Funktion nollakohdat : ne muuttujan arvot, joilla funktion arvo on 0. Nollakohdat saadaankin laskettua ratkaisemalla yhtälö 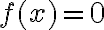 . Nollakohdilla on funktion tutkimisessa tärkeä osa: esimerkiksi funktion arvot voivat muuttua positiivisista negatiivisiksi tai päinvastoin vain sen nollakohdissa, kun funktio on jatkuva.
. Nollakohdilla on funktion tutkimisessa tärkeä osa: esimerkiksi funktion arvot voivat muuttua positiivisista negatiivisiksi tai päinvastoin vain sen nollakohdissa, kun funktio on jatkuva.
Esim. 4. Ratkaise funktion nollakohdat, kun funktion yhtälö on