Funktiota voidaan havainnollistaa piirtämällä sen kuvaaja (x, y)-koordinaatistoon. 

Kuvaajassa jokaisen pisteen x-koordinaatti on muuttujan arvo ja y-koordinaatti sitä vastaava funktion arvo. Jos funktion määrittelyjoukko on koko reaalilukujen joukko 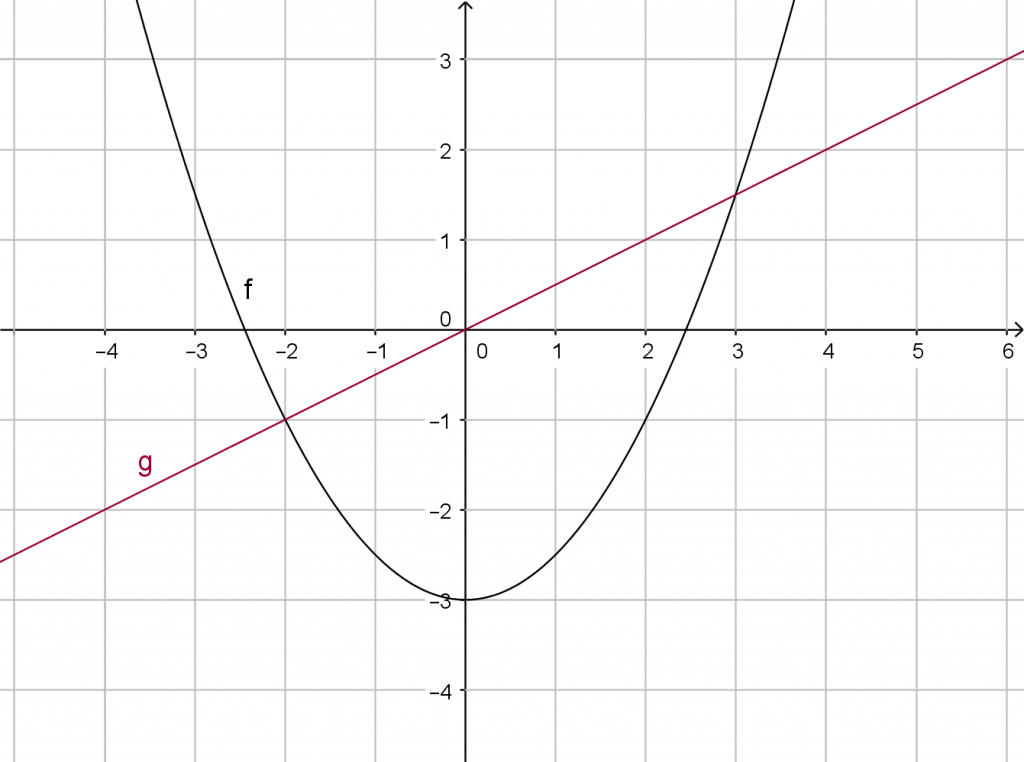, kuvaajaksi tulee katkeamaton käyrä, koska funktio liittää jokaiseen x-akselin pisteeseen yhden y:n arvon.

Kuvaajasta nähdään samoja funktion ominaisuuksia, joita voidaan funktion säännön, lausekkeen avulla laskea, kuten

  • funktion arvo valitulla muuttujan x arvolla
  • annettua funktion arvoa vastaava muuttujan x arvo
  • funktion nollakohdat
  • millä muuttujan x arvoilla funktion arvot ovat positiivisia / negatiivisia (funktion merkki)
  • missä pisteessä funktioiden kuvaajat leikkaavat

\mathbb{R}

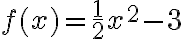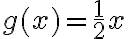Kuvassa on funktioiden  f(x)= \frac{1}{2}x^2-3 ja  g(x)= \frac{1}{2}x kuvaajat.  Katsotaan, miten kuvaajasta näkyvät samat funktion ominaisuudet, joita voi laskea lausekkeen perusteella:



Funktion tulkinta
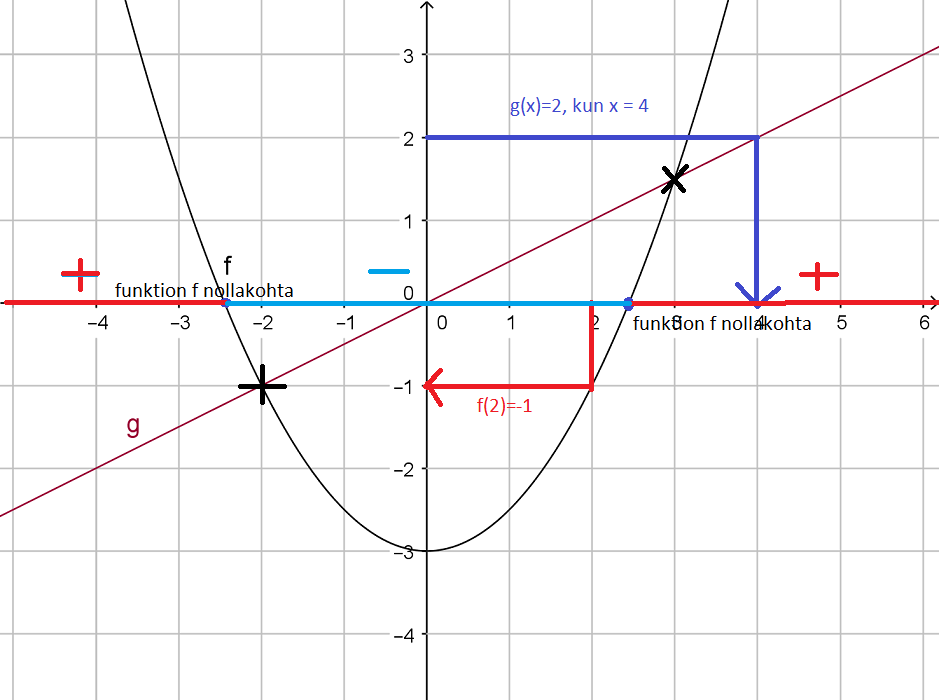
kuvaajasta selvitettävä laskemalla
siirry kohdasta x = 2 kuvaajalle ja lue
vastaava y:n arvo (punainen nuoli), y = -1

 funktion arvo, kun x = 2 f(2) = ½·22-3=-1
siirry kohdasta y = 2 funktion g kuvaajalle ja
lue vastaava x:n arvo (sininen nuoli), x = 4 

 millä x:n arvolla g(x)=2 g(x) = ½x = 2  Ι ·2
               x = 4
nollakohdat ovat ne x:n arvot, joissa kuvaaja
leikkaa x-akselin, kuvaajasta x ≈ ± 2,4

 funktion f nollakohdat ratkaistaan
½x2-3=0     Ι ·2
x2= 6
x = ±√6 ≈ ±Ï2,45
tutkitaan, millä x:n arvoilla funktion kuvaaja
on x-akselin yläpuolella: x < -2,4 tai x > 2,4
(punainen jana)

 millä muuttujan x arvoilla f(x) > 0 ratkaistaan epäyhtälö ½x2-3>0,
saadaan x < -√6 tai x > √6
millä x:n arvoilla funktion kuvaaja on x -akselin alapuolella: -2,4 < x < 2,4
(sininen jana)

 millä muuttujan x arvoilla f(x) < 0 epäyhtälöstä ½x2-3 < 0 saadaan
-√ 6 < x < √ 6
missä pisteissä funktioiden kuvaajat leikkaavat: pisteissä (-2, -1) ja (3; 1,5) missä pisteissä funktiot f ja g saavat saman arvon
  ratkaistaan yhtälö f(x) = g(x):
 ½x2-3 = ½x
saadaan x = -2 ja x = 3
Koska kysytään leikkauspisteitä,
lasketaan vastaavat y-koordinaattien arvot:
x = -2, joten y = ½ ·(-2) = -1
x = 3, joten y = ½ · 3 = 1,5
Vastaus: pisteissä (-2,-1) ja (3; 1,5)

Laskemalla-sarakkeen kolmessa alimmassa kohdassa olevat 2. asteen yhtälöt ja epäyhtälöt opetellaan ratkaisemaan myöhemmillä kursseilla. Jos funktion lauseke on 1. astetta, osaat ratkaista ne jo tässä vaiheessa.
Última modificación: sábado, 16 de noviembre de 2019, 14:12