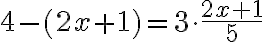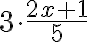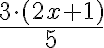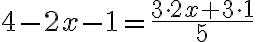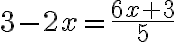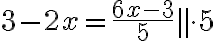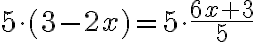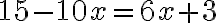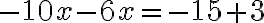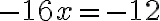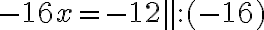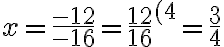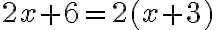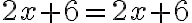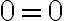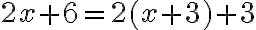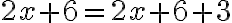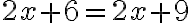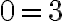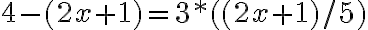Ensimmäisen asteen yhtälöstä ratkaistaan tuntematon siirtämällä muut ensimmäisen asteen termit (eli x:t) yhtälön vasemmalle puolelle ja vakiotermit (eli luvut) yhtälön oikealle puolelle.

Yhtälöstä :

  • avataan sulkeet
  • kerrotaan nimittäjä pois
  • siirretään termit (vähentämällä / lisäämällä niitä kummallekin puolelle yhtäsuuruusmerkkiä) 
  • yhdistellään samanlaiset 
  • jaetaan molemmat puolet yhtälöä mahdollisella x:n kertoimella.

Esimerkki ensimmäisen asteen yhtälön ratkaisemisesta

4-(2x+1)=3 \cdot \frac{2x+1}{5}

avataan sulkeet 


Huomaa, että murtoviivaan pitää suhtautua samalla tavalla kuin sulkeisiin eli oikealla puolella oleva

3 \cdot \frac{2x+1}{5}  
merkintä voisi siis olla myös 

\frac{3 \cdot(2x+1)}{5}

kolmella kertominen kohdistuu siis koko murtolukuun eli osoittajan molemmat termit on kerrottava kolmella 

Huomaa, että jos sulkeiden edessä on - merkki, vaikuttaa se kaikkiin sulkeiden sisällä oleviin termeihin.  Ole tarkkana siis siinä, mitä yhtälön vasemmalla puolella nyt tapahtuu!

4-2x-1 = \frac{3 \cdot2x+3 \cdot1 }{5}

tässä vaiheessa voit jo hieman sieventää yhtälöä yhdistämällä vasemmalla puolella luvut 4 ja -1 sekä laskemalla oikealla puolella kertolaskut

3-2x = \frac{6x+3}{5}

poistetaan nimittäjät

eli kerrotaan yhtälön molemmat puolet nimittäjällä (tai jos niitä on useampia, pienimmällä luvulla, jolla kaikki nimittäjät saadaan pois).

Tämä toimenpide merkitään ensin yhtälön oikealle puolelle kaksoisviivan jälkeen

3-2x= \frac{6x-3}{5} \parallel \cdot5

huomaa lisätä sulkeet vasemmalle puolelle

5 \cdot(3-2x)=5 \cdot \frac{6x+3}{5}

nyt vasemmalla puolella kerrot jälleen sulkeet pois ja oikealla puolella saat supistettua nimittäjän pois

15-10x= 6x+3

siirretään termit ja yhdistetään samanlaiset

Seuraavaksi ensimmäisen asteen muuttujat (eli x:t) siirretään vasemmalle puolelle ja vakiot (eli pelkät luvut) oikealle puolelle yhtälöä. Siirtäminen on teknisesti ottaen vähentämistä tai lisäämistä yhtälön molemmille puolille eli "siirretyn" termin etumerkki vaihtuu sen vaihtaessa yhtäsuuruusmerkin puolelta toiselle.

-10x-6x=-15+3

-16x=-12

 

ratkaistaan x

Nyt jaetaan yhtälön molemmat puolet x:n edessä olevalla kertoimella, jotta saadaan x selville

-16x=-12\parallel :(-16)

x= \frac{-12}{-16}= \frac{12}{16}^{(4}= \frac{3}{4}

 

 

Täältä pääset katsomaan matikkamatskujen videon ensimmäisen asteen yhtälöstä

MITÄ IHMETTÄ?
Entä, jos vastaus onkin muotoa 0 = 0  (pitää toki paikkaansa) tai 5=0 (ei pidä paikkaansa)?

Joskus yhtälön ratkaiseminen johtaa tilanteeseen, jossa saadaan paikkaansa pitävä väite. Tällöin yhtälön sanotaan olevan identtisesti tosi ja se toteutuu kaikilla x:n reaaliarvoilla.

esimerkiksi

2x+6 = 2(x+3)

2x+6 = 2x+6

0=0

toisalta voidaan päätyä omituiseen väittämään esim 4=0 . Tällainen identtisesti epätosi yhtälö ei ole tosi millään x:n arvoilla.

esimerkiksi

2x+6 = 2(x+3)+3

2x+6=2x+6+3

2x+6 =2x+9

0=3

Yhtälön ratkaiseminen GeoGebralla CAS-toiminnoilla
Ratkaistaan ensimmäisenä esimerkkinä ollut yhtälö.

Kirjoita yhtälö ensimmäiselle riville CAS-ruudussa - ole tarkka sulkeiden oikeasta käytöstä erityisesti murtolausekkeiden kohdalla. Kirjoita kaava tässä muodossa ja paina enteriä

4-(2x+1)=3*((2x+1)/5)

Seuraavalle riville kirjoita "ratkaise", jolloin GeoGebra antaa vaihtoehtoja. Valitse ylimmäinen

Sulkeiden sisus jää siniseksi ja saat edelliseltä riviltä suoraan siirrettyä yhtälön siihen klikkaamalla hiirellä ensimmäisen rivin alimmaisena olevaa yhtälöä.

Vastauksen saat joko tarkkana arvona tai likiarvona riippuen siitä mikä valinta sinulla on  ylävalikossa
Modifié le: jeudi 26 mars 2020, 10:30