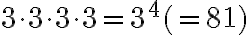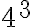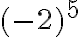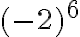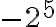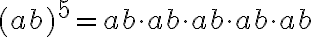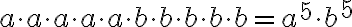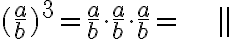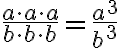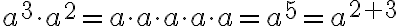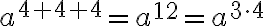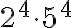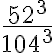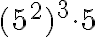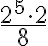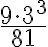Potenssit
Potenssit
POTENSSI
Eksponenttina positiivinen kokonaisluku
Potenssia käytetään lyhempänä merkintätapana, kun samaa lukua kerrotaan itsellään monta kertaa. Esimerkiksi
tarkoittaa, että luku 3 on kerrottu itsellään neljä kertaa. Yleisesti potenssin määritelmä voidaan kirjoittaa
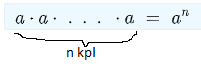 ,
,
missä kantaluku 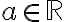 (a on reaaliluku) ja eksponentti n on positiivinen kokonaisluku.
(a on reaaliluku) ja eksponentti n on positiivinen kokonaisluku.
Yleisimpiin eksponentteihin liittyvät erityisnimitykset:
- toinen potenssi on luvun neliö
- kolmas potenssi on luvun kuutio
Esimerkiksi 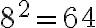 on luvun 8 neliö ja
on luvun 8 neliö ja 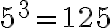 luvun 5 kuutio.
luvun 5 kuutio.
HUOM! Kun merkitset tai lasket lukujen potenssiinkorotuksia, sulkujen paikka on tärkeää ottaa huomioon. Esimerkiksi 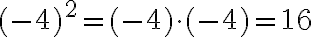 , mutta
, mutta 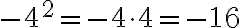 . Suluilla osoitetaan, kuuluuko -merkki kantalukuun, kuten ensimmäisessä tapauksessa, vai onko se kantaluvusta erillään, kuten jälkimmäisessä tapauksessa.
. Suluilla osoitetaan, kuuluuko -merkki kantalukuun, kuten ensimmäisessä tapauksessa, vai onko se kantaluvusta erillään, kuten jälkimmäisessä tapauksessa.
Pohdi esimerkkiä. Ratkaisu löytyy tarvittaessa tiedostona alempaa
Esimerkki 1 Laske
Potenssien laskusäännöt
Kerrataan potenssien laskusäännöt, koska niitä tarvitaan jatkossa mm. polynomilaskuissa ja jo myöhemmin tällä kurssilla eksponenttiyhtälöiden ratkaisemisessa. Potenssikaavoja voit käyttää tilanteen mukaan molempiin suuntiin, vasemmalta oikealle ja oikealta vasemmalle.
- Tulon potenssi:
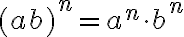
- Osamäärän potenssi:
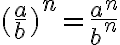
- Samankantaisten potenssien tulo:
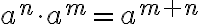
- Samankantaisten potenssien osamäärä:
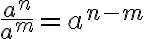
- Potenssin potenssi:
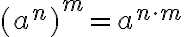
Perustellaan laskusäännöt:
Tulon potenssi:
Tarkastellaan esimerkiksi lauseketta 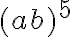 . Potenssin määritelmän mukaan
. Potenssin määritelmän mukaan
Osamäärän potenssi:
Tarkastellaan esimerkiksi lauseketta 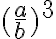 . Potenssin määritelmän mukaan
. Potenssin määritelmän mukaan
Tätä kaavaa käytetään, kun korotetaan murtolukuja tai -lausekkeita potenssiin. Esimerkiksi 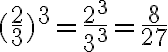 .
.
Samankantaisten potenssien tulo:
Tarkastellaan esimerkiksi lauseketta 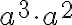 . Tämä on samankantaisten potenssien tulo, koska molemmissa tulontekijöissä on sama kantaluku, tällä kertaa a. Potenssin määritelmän mukaan
. Tämä on samankantaisten potenssien tulo, koska molemmissa tulontekijöissä on sama kantaluku, tällä kertaa a. Potenssin määritelmän mukaan 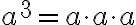 ja
ja 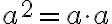 , joten
, joten
Tätä kaavaa tarvitaan viimeistään polynomien sieventämisessä. Esimerkiksi 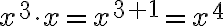
Samankantaisten potenssien osamäärä:
Tarkastellaan esimerkiksi lauseketta 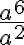 . Potenssin määritelmän mukaan
. Potenssin määritelmän mukaan 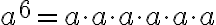 ja
ja 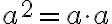 , joten
, joten
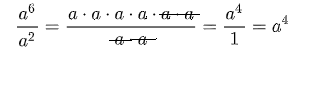
Samankantaisten potenssien osamäärän kaavaa käytetään ainakin, kun sievennetään polynomien jakolaskuja.
Potenssin potenssi:
Tarkastellaan esimerkiksi lauseketta 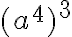 . Potenssin määritelmän mukaan
. Potenssin määritelmän mukaan
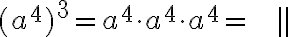 Samankantaisten potenssien tulo
Samankantaisten potenssien tulo
Pohdi potenssien laskusääntöjen perusteella seuraavia esimerkkejä:
Esimerkki 2: Laske
Esimerkki 3: Ilmaise