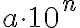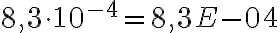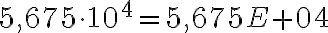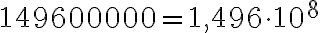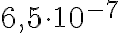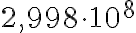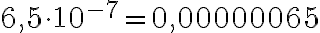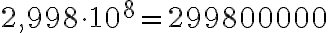Kymmenpotenssimuoto
Kymmenpotenssimuoto
KYMMENPOTENSSIMUOTO
Erityisesti kemiassa ja fysiikassa tutkitaan niin pieniä (kuten protonin massa 0,0000000000000000000000000017 kg) ja toisaalta suuria (kuten Maan etäisyys Auringosta 149 600 000 km) lukuja, että ne on havainnollisempaa merkitä kymmenpotenssimuodossa eli käyttää tieteellistä merkintätapaa. Myös todennäköisyyslaskennassa todenäköisyydet voivat olla hyvin pieniä tai mahdollisten vaihtoehtojen määrät todella suuria.
Kymmenpotenssimuoto tarkoittaa, että luvut voidaan kirjoittaa myös muodossa
missä a on luku väliltä 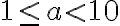 ja kymmenen potenssi n on kokonaisluku.
ja kymmenen potenssi n on kokonaisluku.
Tätä merkintää käyttäen esimerkiksi luku 56750 on 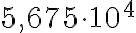 , mikä pitää paikkansa, koska
, mikä pitää paikkansa, koska 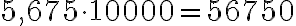 . Luku 0,00083 puolestaan on
. Luku 0,00083 puolestaan on 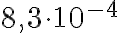 , ja se on totta, koska
, ja se on totta, koska 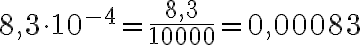 .
.
Laskimessa edellä saadut kymmenpotenssimuodot saattavat näyttää (laskimesta riippuen) hämäävästi vaikkapa tältä :
Luvusta kymmenpotenssimuotoon
Oikea kymmenen eksponentti n löytyy, kun lasketaan, kuinka monen numeron yli desimaalipilkkua täytyy muunnoksessa siirtää. Muutetaan kymmenpotenssimuotoon alussa mainitut protonin massa ja Auringon ja Maan välinen etäisyys.
Esimerkki 6: a) Protonin massa on siis noin 0,0000000000000000000000000017 kg. Ensimmäinen nollasta eroava numero on pilkun jälkeen 27. numero, luku 1. Kerroin kymmenpotenssimuodossa on tässä tapauksessa 1,7. Kun desimaalipilkku siirretään alkuperäiseltä paikaltaan lukujen 1 ja 7 väliin, on sitä siirretty 27 numeron yli oikealle. Muutettaessa luvusta kymmenpotenssimuotoon oikealle siirtäminen merkitsee negatiivista eksponenttia kymmenelle. Saadaan kymmenpotenssimuodoksi 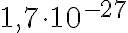
b) Maan ja Auringon etäisyys on 149 600 000 km. Kertoimeksi halutaan luku 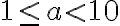 , joten tässä tapauksessa se on 1,496, jos lukua ei haluta pyöristää enempää. Desimaalipilkkua ei näy luvussa, mutta tiedämme, että se on periaatteessa viimeisen näkyvän nollan eli ykkösten jälkeen. Desimaalipilkkua siirretään siis tällä kertaa vasemmalle 8 numeron yli. Muutettaessa luvusta kymmenpotenssimuotoon vasemmalle siirtäminen merkitsee positiivista eksponenttia. Saadaan
, joten tässä tapauksessa se on 1,496, jos lukua ei haluta pyöristää enempää. Desimaalipilkkua ei näy luvussa, mutta tiedämme, että se on periaatteessa viimeisen näkyvän nollan eli ykkösten jälkeen. Desimaalipilkkua siirretään siis tällä kertaa vasemmalle 8 numeron yli. Muutettaessa luvusta kymmenpotenssimuotoon vasemmalle siirtäminen merkitsee positiivista eksponenttia. Saadaan
Kymmenpotenssimuodosta luvuksi
Kymmenen eksponentista nähdään tässä tapauksessa, kuinka monen numeron yli desimaalipilkkua tulee siirtää ja mihin suuntaan.
Esmerkki 7: Kirjoita ilman kymmenpotenssia
a) Koska kymmenen eksponentti on -7, siirretään pilkkua 7 numeron yli vasemmalle muutoksessa kymmenpotenssimuodosta luvuksi. Saadaan
b) Koska kymmenen eksponentti on +8, muutoksessa kymmenpotenssimuodosta luvuksi siirretään pilkkua 8 numeron yli oikealle. Pilkun jälkeen kertoimessa on vain kolme numeroa, mutta lisätään loppuun tarpeellinen määrä nollia, nyt 5. Saadaan