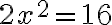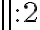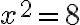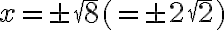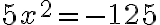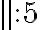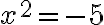Potenssiyhtälön ratkaiseminen
Potenssiyhtälön ratkaiseminen
Potenssiyhtälön perusmuoto on 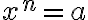 . Esimerkiksi yhtälöt
. Esimerkiksi yhtälöt 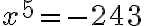 ja
ja 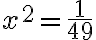 ovat potenssiyhtälöitä. Potenssifunktioiden kuvaajia tarkasteltaessa huomattiin, että funktion ominaisuudet riippuvat siitä, onko eksponentti n parillinen vai pariton. Myös potenssiyhtälöä ratkaistaessa funktioiden erilaiset ominaisuudet on otettava huomioon.
ovat potenssiyhtälöitä. Potenssifunktioiden kuvaajia tarkasteltaessa huomattiin, että funktion ominaisuudet riippuvat siitä, onko eksponentti n parillinen vai pariton. Myös potenssiyhtälöä ratkaistaessa funktioiden erilaiset ominaisuudet on otettava huomioon.
Tarkastellaan esimerkiksi yhtälöitä
PARITON EKSPONENTTI
a) yhtälössä 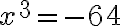 kysytään, mikä luku on korotettava kolmanteen potenssiin, että saadaan -64. Tämä sama kysymys liittyi myös kuutiojuureen. Yhtälön ratkaisu saadaankin ottamalla yhtälöstä puolittain kuutiojuuri (kolmas juuri):
kysytään, mikä luku on korotettava kolmanteen potenssiin, että saadaan -64. Tämä sama kysymys liittyi myös kuutiojuureen. Yhtälön ratkaisu saadaankin ottamalla yhtälöstä puolittain kuutiojuuri (kolmas juuri):
Kuvassa on funktion 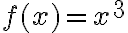 kuvaaja. Kuvaajan perusteella funktio saa arvon -64 vain, kun x = -4.
kuvaaja. Kuvaajan perusteella funktio saa arvon -64 vain, kun x = -4.
Yhtälö voidaan ratkaista, koska negatiivisillakin luvuilla on kuutiojuuri. Ratkaisuja on yksi, x = -4.
PARILLINEN EKSPONENTTI
b) Yhtälöä 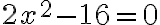 pitää ensin muokata niin, että toiselle puolelle jää vain
pitää ensin muokata niin, että toiselle puolelle jää vain 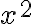 ja toiselle puolelle luku. Jos yhtälö saadaan tällaiseen muotoon, se on potenssiyhtälö ja ratkaisu löytyy juurella. Siirretään siis -16 yhtälön oikealle puolelle:
ja toiselle puolelle luku. Jos yhtälö saadaan tällaiseen muotoon, se on potenssiyhtälö ja ratkaisu löytyy juurella. Siirretään siis -16 yhtälön oikealle puolelle:
Tarkastellaan tässä vaiheessa funktion 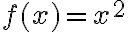 kuvaajaa.
kuvaajaa.
Kuvaajan perusteella funktio saa arvon kahdella muuttujan x arvolla, joiden likiarvot ovat kuvaajan perusteella 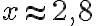 ja
ja 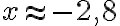 .
.
Yhtälö ratkaistaan ottamalla molemmilta puolilta toinen juuri eli neliöjuuri. Koska neliöjuuri on määritelmän mukaan aina positiivinen, mutta yhtälölle pitäisi löytää kaikki ratkaisut, siis myös negatiivinen, on neliöjuurimerkin eteen merkittävä 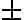 , joka tarkoittaa, että ratkaisuja tulee kaksi, sekä neliöjuuri että sen vastaluku. Saadaan tarkaksi vastaukseksi
, joka tarkoittaa, että ratkaisuja tulee kaksi, sekä neliöjuuri että sen vastaluku. Saadaan tarkaksi vastaukseksi
Tämä vastaus on tarkka ja pitää ainakin olla näkyvillä. Lisäksi likiarvon saa laskimella.
c) Yhtälön 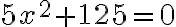 ratkaiseminen aloitetaan jälleen muokkaamalla yhtälö muotoon
ratkaiseminen aloitetaan jälleen muokkaamalla yhtälö muotoon 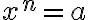 . Saadaan:
. Saadaan:
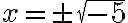 , mutta negatiivisella luvulla ei ole neliöjuurta, joten yhtälöllä ei ole ratkaisua.
, mutta negatiivisella luvulla ei ole neliöjuurta, joten yhtälöllä ei ole ratkaisua.
Potenssiyhtälön 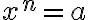 ratkaiseminen:
ratkaiseminen:
- n on pariton. Yhtälöllä on aina yksi ratkaisu
![x= \sqrt[n]{a} x= \sqrt[n]{a}](https://edugo.fi/filter/tex/pix.php/06c69911b9f96c84d71e150ae0953b26.gif)
- n on parillinen. Kun
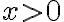 , yhtälöllä on kaksi ratkaisua,
, yhtälöllä on kaksi ratkaisua, ![x = \pm \sqrt[n]{a} x = \pm \sqrt[n]{a}](https://edugo.fi/filter/tex/pix.php/20b5eca325d589beb81a2ae7806d855f.gif) . Kun
. Kun 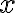 , yhtälöllä ei ole ratkaisua. Erikoistapauksessa x = 0 ratkaisuja on yksi.
, yhtälöllä ei ole ratkaisua. Erikoistapauksessa x = 0 ratkaisuja on yksi.
![x= \sqrt[3]{-64}=-4 x= \sqrt[3]{-64}=-4](https://edugo.fi/filter/tex/pix.php/49fc0700f1dad0cb775d3c67baefff3e.gif)