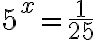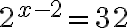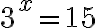Eksponenttiyhtälö

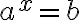Eksponenttiyhtälössä  a^x=b  tuntematon x onkin eksponentissa. Esimerkiksi yhtälö  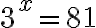3^x=81  on eksponenttiyhtälö.  

Eksponenttiyhtälöä ei voi ratkaista kaikilla luvuilla: ehtona on, että kantaluvun a on oltava positiivinen luku, mutta ei luku 1. Lisäksi ratkaisu löytyy vain, jos myös toinen puoli, siis luku b on positiivinen.


Pohdi tätä

Eksponenttiyhtälön ratkaisemiseen meillä ei ole vielä työkaluja.

Pohdi, mikä luku (tai mitkä luvut) x toteuttaisi seuraavat eksponenttiyhtälöt:

  1. 3^x=81
  2. 5^x= \frac{1}{25}
  3. 2^{x-2}=32

Ratkaisu löytyy alla olevalta videolta

Eksponenttiyhtälön ratkaiseminen


Eksponenttiyhtälön ratkaisemiseen on kaksi mahdollisuutta. Ensimmäinen on etsiä yhtälön molemmille puolille sama kantaluku, jolloin yhtälöstä tulee tosi vain eksponenttien ollessa yhtä suuret. Ratkaisu löytyi yllä olevissa yhtälöissä näin. Saman kantaluvun löytämiseksi on yhtälöä usein muokattava potenssien laskusääntöjä käyttäen. Siitä huolimatta on aika harvinaista, että sama kantaluku löytyisi molemmille yhtälön puolille.


Entä jos samaa kantalukua ei ole mahdollista löytää?


Tarkastellaan yhtälöä   3^x=15 . 

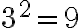Koska   3^2=9 , ratkaisun on oltava suurempi kuin luku 2.

Mutta 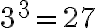  3^3=27 , joka on liian paljon.  Ratkaisu on siis pienempi kuin 3. Tässä tapauksessa molemmille puolille sopivaa samaa kantalukua ei löydy. Tutkitaan toista ratkaisumahdollisuutta.

Piirretään  funktion 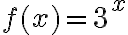  f(x)=3^x   kuvaaja Geogebralla. Video on alla: Eksponenttiyhtälön graafinen ratkaiseminen.

Varsinaisesti eksponentti saadaan ratkaistua Logaritmin avulla, josta lisää videon jälkeen 
Последнее изменение: суббота, 19 октябрь 2019, 20:23