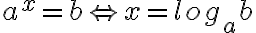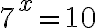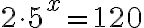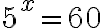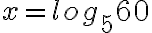Logaritmi

Logaritmin määritelmä:

$a^x=b \Leftrightarrow x=log _a b$

Logaritmi vastaa kysymykseen: Mihin potenssiin kantaluku a on korotettava, jotta saadaan b?

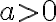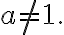Rajoitukset: kantaluku $a > 0$  ja $a \neq 1.$ Myös luvun b on oltava positiivinen. 

Tarkastellaan yhtälön 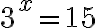 $3^x=15$ logaritmiratkaisua. 

Logaritmin määritelmän mukaan käytetään 3-kantaista logaritmia ja logaritmoitava on 15. Saadaan tarkka ratkaisu 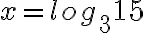 $x=log_3 15$. 

Ratkaisu on kokonaisuus ja se tarkoittaa lukua, jolle likiarvo saadaan esimerkiksi laskimesta. Kokonaisuutta 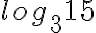$log_3 15$ ei voi hajottaa osiin.

Esimerkki: Ratkaise yhtälöt

a)  $7^x=10$

Sovelletaan logaritmin määritelmää. Kantaluku on 7, koska potenssin kantaluku on 7. Logaritmoitava on 10. Saadaan tarkka ratkaisu: 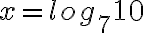 $x=log_7 10$. 

b)  $2 \cdot 5^x=120$

Emme voi vielä soveltaa logaritmin määritelmää, kun termin 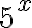$5^x$ edessä on kerroin 2. 

Kertolaskua 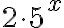$2 \cdot5^x$ ei voi tehdä, koska potenssiin korotus on laskujärjestyksessä ennen kertolaskua. Muista siis: kantalukuun ei saa koskea. Kertoimesta päästään eroon jakamalla luvulla 2. Saadaan:

$5^x=60$

Nyt ratkaisu logaritmin määritelmän mukaan onnistuu. Kantaluku on potenssin kantaluku 5 ja logaritmoitava 60. Tarkka ratkaisu:

$x=log_5 60$

Allaolevassa videossa katsotaan, miten likiarvot saa määritettyä Geogebralla.

Lisätietoa logaritmeista

Käytännössä useimmin käytettävät logaritmit ovat

• luonnollinen logaritmi ln, jonka kantaluku on Neperin luku e ≈ 2,7183. Yhtälön 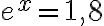 $e^x=1,8$  ratkaisu on logaritmin määritelmän mukaan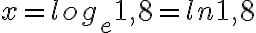  $x = log_e 1,8 = ln1,8$
• Briggsin logaritmi lg, jonka kantaluku on 10. Yhtälön 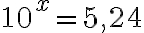 $10^x = 5,24$ ratkaisu on logaritmin määritelmän mukaan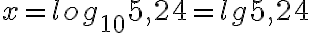  $x = log_{10} 5,24 = lg 5,24$

Laskimissa on usein näppäin ln, jolla saa luonnollisen logaritmin ja näppäimellä log saa 10-kantaisen logaritmin. Alimpana olevassa videossa ratkaistaan eksponenttiyhtälö käyttämällä 10-kantaista logaritmia lg.