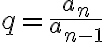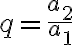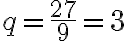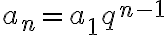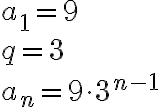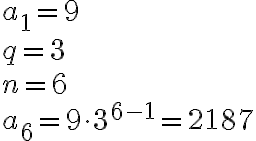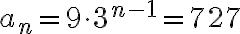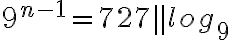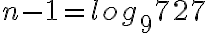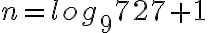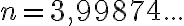Geometrinen lukujono

Geometrisen lukujonon kahden perättäisen termin suhde on aina vakio. 

9, 27, 81, 243, 729,...

Tätä jakamalla saatavaa lukua kutsutaan suhdeluvuksi

$q = \frac{a_n}{a_{n-1}$

Tälle esimerkkinä olevalle lukujonolle suhdeluvuksi saadaan

$q = \frac{a_2}{a_1}$

$q = \frac{27}{9}=3$

Yleinen jäsen geometriselle lukujonolle saadaan, kun tiedetään suhdeluku ja ensimmäinen jäsen.

$a_n=a_1q^{n-1}$

Eli tälle esimerkkinä olevalle lukujonolle

$a_1=9\\ q=3\\ a_n=9 \cdot 3^{n-1}$

Näin lukujonon kuudes termi saataisiin laskettua seuraavasti

$a_1=9\\ q=3\\ n=6\\ a_6=9 \cdot 3^{6-1} = 2187$

Lukujonon yleisen jäsenen kaavalla voidaan myös tutkia monesko joku luku on lukujonossa tai kuuluuko se ensinkään kyseiseen lukujonoon. Tarkastellaan esimerkiksi lukua 727.

$a_n=9 \cdot 3^{n-1} =727$

$9^{n-1}= 727 \parallel log_9$

$n-1=log_9727$

$n=log_9727+1$

$n= 3,99874...$

Koska vastaus ei ole kokonaisluku, luku 727 ei kuulu lukujonoon.

Oheisesta linkistä pääset katsomaan Matikkamatskut videon geometrisestä lukujonosta